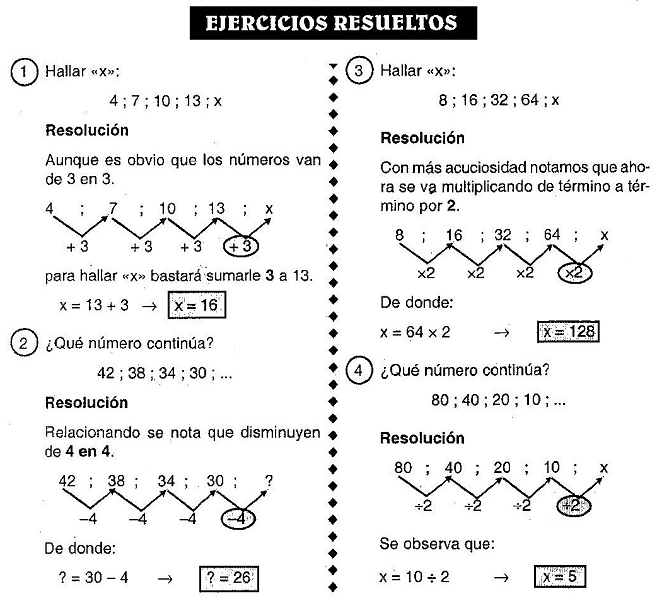
Sucesiones Matemáticas
Sucesiones Matemáticas
Por el libro, una sucesión se define como una aplicación definida sobre los números naturales (1,2,3,...). Dicho así, la definición enciclopédica puede resultar un poco confusa. Dicho con palabras llanas, una sucesión es un conjunto infinito de números ordenados que se suceden siguiendo alguna lógica. Si alguien ha hecho en su vida algún test de inteligencia, está relacionado con los típicos juegos de adivinar el siguiente número.
Un ejemplo de sucesión sería este
X1 = 1
X2 = 3
X3 = 5
.....
siendo el término n-ésimo:
Xn = 2·n - 1
Esta sucesión representa a los números impares. A simple vista se puede ver que desde el punto de vista de la notación, la sucesión presenta una enorme ventaja. Permite expresar infinitos números en una expresión muy corta. En el caso del ejemplo anterior:
f(n) = 2·n - 1
Si sustituimos el término n por cualquier valor natural obtenemos automáticamente el término correspondiente de la sucesión. Como sucede con otras herramientas, como las matrices, la sucesión permite abreviar notablemente las expresiones y ahorrar en cálculos.
Las aplicaciones de las sucesiones son incontables. Se utilizan abundantemente para demostrar los teoremas y las propiedades de la topología matemática, y en la muy conocida demostración del número pi, pero dado que esta parte del cálculo es la más inocua, son mucho más destacadas sus aplicaciones en materia de cálculo numérico.
Las series numéricas son la suma de los términos de una sucesión y la materia más densa de la primera parte de la asignatura cálculo del primer curso de cualquier carrera técnica. Existen varios tipos de series en función de la naturaleza de la sucesión que las conforma, que pueden ser aritméticas, geométricas, basadas en funciones trigonométricas, logarítmicas, exponenciales, etcétera... Pues calcular la suma de términos de las sucesiones es de aplicación para calcular el error máximo que obtenemos al realizar una operación por un método de cálculo numérico iterativo.
Bajaré a la tierra por un momento. Imaginemos esta sucesión, de tipo geométrico, definida de forma implícita:
Xn = X(n-1) / 2,
con X1=1
y donde X(n-1) es el término anterior a Xn
Cada término es la mitad del término anterior
Xn = 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128....
Se puede demostrar mediante la teoría de series que cada término es igual a la suma de todos los siguientes. Por lo tanto, si calculamos "a groso modo" una suma de números de este tipo sumando los términos uno a uno, podemos acotar el error que se produce, que puede ser todo lo pequeño que queramos a costa de invertir más tiempo sumando números. Si queremos que el error sea menor del 1% bastaría con sumar todos los términos hasta que llegar a un término inferior a 1/100, concretamente los 8 primeros del ejemplo expuesto. Esta es la forma concreta en la que "piensa" y resuelve los problemas complejos (integración, resolución de sistemas) una calculadora o un ordenador.
Imaginemos que le damos la vuelta a la sucesión y trabajamos con:
Xn = X(n-1) · 2
X1 = 1
Xn = 1, 2, 4, 8, 16, 32, 64, 128,....
Aquí, del mismo modo, cada término es igual a la suma de todos los números situados a la izquierda más el primer término. Por definición de sucesión cada término debe de ser inequívoco y por lo tanto el primer término debe de ser una constante. Si el primer término fuese infinitamente pequeño (infinitésimo), para los efectos sí que se daría como en el caso anterior que cada término es igual al caso anterior. Por tanto, si en un juego de apuestas en el que el payoff es igual al riesgo y la cantidad inicial es un número cualquiera de esta sucesión, si cada vez que perdiésemos volviésemos a jugar la cantidad del siguiente número de la sucesión hasta ganar, y suponiendo que no sufrimos una cantidad infinita de derrotas, nuestro beneficio sería siempre el mismo y exactamente igual a la primera cantidad apostada.
La principal aplicación de esto son los juegos. Nos encontramos ante un sistema de tipo martingale

¿Qué es una sucesión?
Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.
 |
Finita o infinita
Si la sucesión sigue para siempre, es una sucesión infinita,
si no es una sucesión finita
Ejemplos
{1, 2, 3, 4 ,...} es una sucesión muy simple (y es una sucesión infinita)
{20, 25, 30, 35, ...} también es una sucesión infinita
{1, 3, 5, 7} es la sucesión de los 4 primeros números impares (y es una sucesión infinita)
{4, 3, 2, 1} va de 4 a 1 hacia atrás
{1, 2, 4, 8, 16, 32, ...} es una sucesión infinita donde vamos doblando cada término
{a, b, c, d, e} es la sucesión de las 5 primeras letras en order alfabético
{a, l, f, r, e, d, o} es la sucesión de las letras en el nombre "alfredo"
{0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s (sí, siguen un orden, en este caso un orden alternativo)
En orden
Cuando decimos que los términos están "en orden", ¡nosotros somos los que decimos qué orden! Podría ser adelante, atrás... o alternando... ¡o el que quieras!
Una sucesión es muy parecida a un conjunto, pero con los términos en orden (y el mismo valor sí puede aparecer muchas veces).
Ejemplo: {0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s. El conjunto sería sólo {0,1}
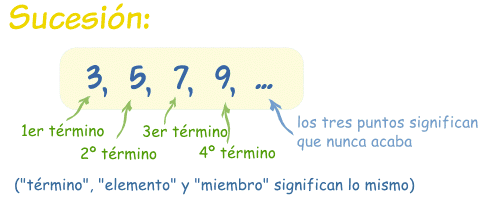
La regla
Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.
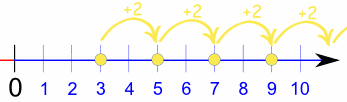
Ejemplo: la sucesión {3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:
¡Pero la regla debería ser una fórmula!
Decir que "empieza por 3 y salta 2 cada vez" no nos dice cómo se calcula el:
- 10º término,
- 100º término, o
- n-ésimo término (donde n puede ser cualquier número positivo que queramos).
Así que queremos una fórmula con "n" dentro (donde n será la posición que tiene el término).
Entonces, ¿cuál sería la regla para {3, 5, 7, 9, ...}?
Primero, vemos que la sucesión sube 2 cada vez, así que podemos adivinar que la regla va a ser "2 × n". Vamos a verlo:
Probamos la regla: 2n
| n | Término | Prueba |
|---|---|---|
| 1 | 3 | 2n = 2×1 = 2 |
| 2 | 5 | 2n = 2×2 = 4 |
| 3 | 7 | 2n = 2×3 = 6 |
Esto casi funciona... pero la regla da todo el tiempo valores 1 unidad menos de lo que debería, así que vamos a cambiarla un poco:
Probamos la regla: 2n+1
| n | Término | Regla |
|---|---|---|
| 1 | 3 | 2n+1 = 2×1 + 1 = 3 |
| 2 | 5 | 2n+1 = 2×2 + 1 = 5 |
| 3 | 7 | 2n+1 = 2×3 + 1 = 7 |
¡Funciona!
Así que en vez de decir "empieza por 3 y salta 2 cada vez" escribimos la regla como
La regla para {3, 5, 7, 9, ...} es: 2n+1
Ahora, por ejemplo, podemos calcular el término 100º: 2 × 100 + 1 = 201
Notación
Para que sea más fácil escribir las reglas, normalmente lo hacemos así:
Posición del término |
|
 |
Es normal usar xn para los términos:
|
| Así que para hablar del "quinto término" sólo tienes que escribir: x5 |
Entonces podemos escribir la regla para {3, 5, 7, 9, ...} en forma de ecuación, así:
xn = 2n+1
Ahora, si queremos calcular el 10º término, podemos escribir:
x10 = 2n+1 = 2×10+1 = 21
¿Puedes calcular el 50º término? ¿Y el 500º?
Ahora veamos algunas sucesiones especiales y sus reglas:
Tipos de sucesiones
Sucesiones aritméticas
El ejemplo que acabamos de usar, {3,5,7,9,...}, es una sucesión aritmética (o progresión aritmética), porque la diferencia entre un término y el siguiente es una constante.
Ejemplos
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
La regla es xn = 3n-2
| 3, 8, 13, 18, 23, 28, 33, 38, ... |
La regla es xn = 5n-2
Sucesiones geométricas
En una sucesión geométrica cada término se calcula multiplicando el anterior por un número fijo.
Ejemplos:
| 2, 4, 8, 16, 32, 64, 128, 256, ... |
La regla es xn = 2n
| 3, 9, 27, 81, 243, 729, 2187, ... |
La regla es xn = 3n
| 4, 2, 1, 0.5, 0.25, ... |
La regla es xn = 4 × 2-n
Sucesiones especiales
Números triangulares
| 1, 3, 6, 10, 15, 21, 28, 36, 45, ... |
Esta sucesión se genera a partir de una pauta de puntos en un triángulo.
Añadiendo otra fila de puntos y contando el total encontramos el siguiente número de la sucesión.
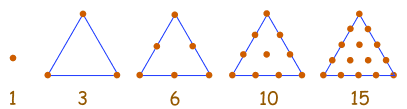
Pero es más fácil usar la regla
xn = n(n+1)/2
Ejemplo:
- El quinto número triangular es x5 = 5(5+1)/2 = 15,
- y el sexto es x6 = 6(6+1)/2 = 21
Números cuadrados
| 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
El siguiente número se calcula elevando al cuadrado su posición.
La regla es xn = n2
Números cúbicos
| 1, 8, 27, 64, 125, 216, 343, 512, 729, ... |
El siguiente número se calcula elevando al cubo su posición.
La regla es xn = n3
Números de Fibonacci
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... |
El siguiente número se calcula sumando los dos que están antes de él.
El 2 se calcula sumando los dos delante de él (1+1)
El 21 se calcula sumando los dos delante de él (8+13)
La regla es xn = xn-1 + xn-2
Esta regla es interesante porque depende de los valores de los términos anteriores.
Por ejemplo el 6º término se calcularía así:
x6 = x6-1 + x6-2 = x5 + x4 = 5 + 3 = 8
Series
"Sucesiones" y "series" pueden parecer la misma cosa... pero en realidad una serie es la suma de una sucesión.
Sucesión: {1,2,3,4}
Serie: 1+2+3+4 = 10
Las series se suelen escribir con el símbolo Σ que significa "súmalos todos":
| Esto significa "suma de 1 a 4" = 10 | |
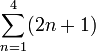 |
Esto significa "suma los cuatro primeros términos de la sucesión 2n+1" Que son los cuatro primeros términos de nuestro ejemplo {3,5,7,9,...} = 3+5+7+9 = 24 |
[Sucesiones Numéricas]
a) 2; 4; 6; 8 ...
b) -1; 2; -3; 4; -5 ...
c)  son sucesiones numéricas
son sucesiones numéricas
|
» Los términos de una sucesión siguen una "regularidad" o "ley" que las caracteriza, que se expresa mediante una fórmula a la que llamamos
término general o término enésimo de la sucesión.
En nuestro ejemplo, el término que ocupa el lugar n es: an = 2.n
En el tercer ejemplo el término general es:

y dando valores a n podemos construir la sucesión:



